7.1. The objective of machine learning¶
Basically, ML tasks tend to fall into two sets of tasks:
Prediction accuracy (e.g. of the label or the group detection)
Feature selection (which X variables and non-linearities should be in the model)
And for both of those, the idea is that what the model learns will work out-of-sample. In the framework of our machine learning workflow, what this means is that after we pick our model in step 5, we only get one chance to apply it on test data and then will move to production models. We want our model to perform as well at step 6 and in production as it does while we train it!
Key takeaway #1
The key to understanding most of the choices you make in a ML project is to remember: The focus of ML is to learn something that generalizes outside of the data we have already!
Econometrically, the goal is to estimate a model on a sample (the data we have) that works on the population (all of the data that can and will be generated in the real world).
7.1.1. Model Risk¶
A model will create predictions, and those predictions will be wrong to some degree when we generalize outside our initial data.
It turns out we can decompose the expected error of a model like this1
Let’s define those terms:
“Model bias”
Def: Is errors stemming from the model’s assumptions in how it predicts the outcome variable. (It is the opposite of model accuracy.)
Complexity helps: Adding more variables or polynomial transformations of existing variables will usually reduce bias
Adding more data to the training dataset can (but might not) reduce bias
“Model variance”
Def: Is extent to which estimated model varies from sample to sample
Complexity hurts: Adding more variables or polynomial transformations of existing variables will usually increase model variance
Adding more data to the training dataset will reduce variance
Noise
Def: Randomness in the data generating process beyond our understanding
To reduce the noise term, you need more data, better data collection, and more accurate measurements
7.1.2. The bias-variance tradeoff¶
Key takeaway #2
Changing the complexity of a model changes the model’s bias and variance, and there is an optimal amount of complexity.
THE FUNDAMENTAL TRADEOFF: Increasing model complexity increases its variance but reduces its bias
Models that are too simple have high bias but low variance
Models that are too complex have the opposite problem
Collecting a TON of data can allow you to use complex models with less variance
This is the essence of the bias-variance tradeoff, a fundamental issue that we face in choosing models for prediction.”2
Let’s work through these ideas visually in the next three tabs:
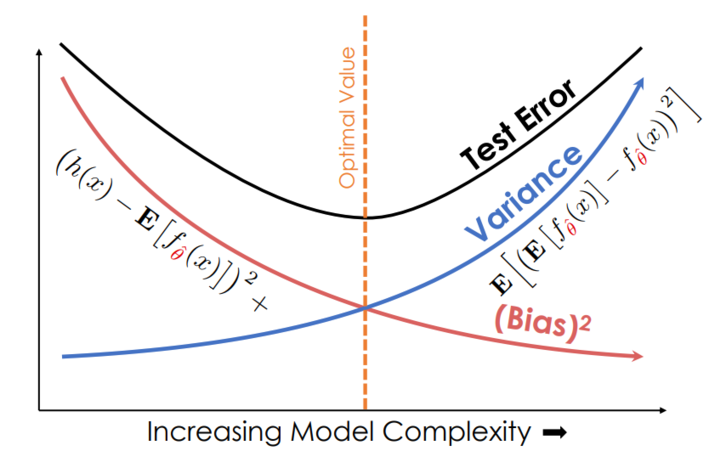
We want to minimize model risk. In the graph below, that is called “Test Error”.
Models that are too simple are said to be “underfit” (take steps to reduce bias)
In the graph below, an underfit model is on the left side of the picture
Models that are too complicated are said to be “overfit” (take steps to reduce variance)
In the graph below, an overfit model is on the right side of the picture
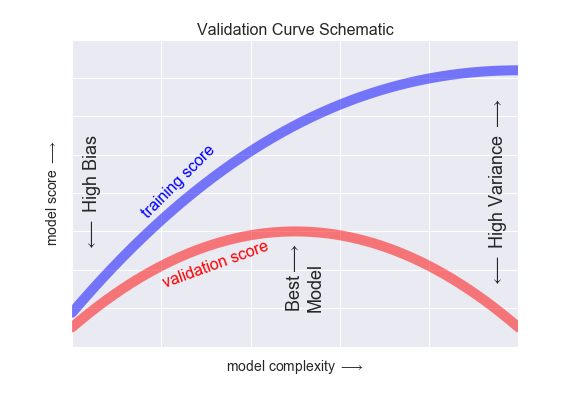
In the chart below, the blue line depicts how well your model does on the “training sample”, meaning: The data the model is trained on. The red line shows how well your model does on data it has never seen before, a so-called “validation sample”.
Models that are too simple perform poorly (low scores, high bias)
Models that are too complex perform well in training but poorly outside that sample (high variance, the gap between the lines)
7.1.3. Minimizing model risk¶
Our tools to minimize model risk are
More data! (Often helps, but not always.)
Proper model evaluation procedures (via cross validation (CV) or out-of-sample (OOS) forecasting) can help gauge whether a model is overfit or underfit.
Feature engineering (adding, cleaning, and selecting features; dimensionality reduction)
Model selection - picking the right model for your setting
I added some good external resources in the links above on feature engineering and model selection. The next pages here will dig into model evaluation because it gets at the flow of testing a model.
