6.3. Goodness of Fit¶
Revisiting the regression objectives: After this page,
- You can measure the goodness of fit on a regression
R\(^2\) and Adjusted R\(^2\)
\(R^2 = 1-SSE/TSS\) = The fraction of variation in y that a model can explain, and always between 0 and 1.
Adding extra variables to a model can not reduce R\(^2\) even if the variables are random
Adjusted R\(^2\) adjusts R\(^2\) by penalizing based on the number of variables in X. It can actually be negative.
sm_ols(<model and data>).fit().summary()automatically reports R\(^2\) and Adjusted R\(^2\)
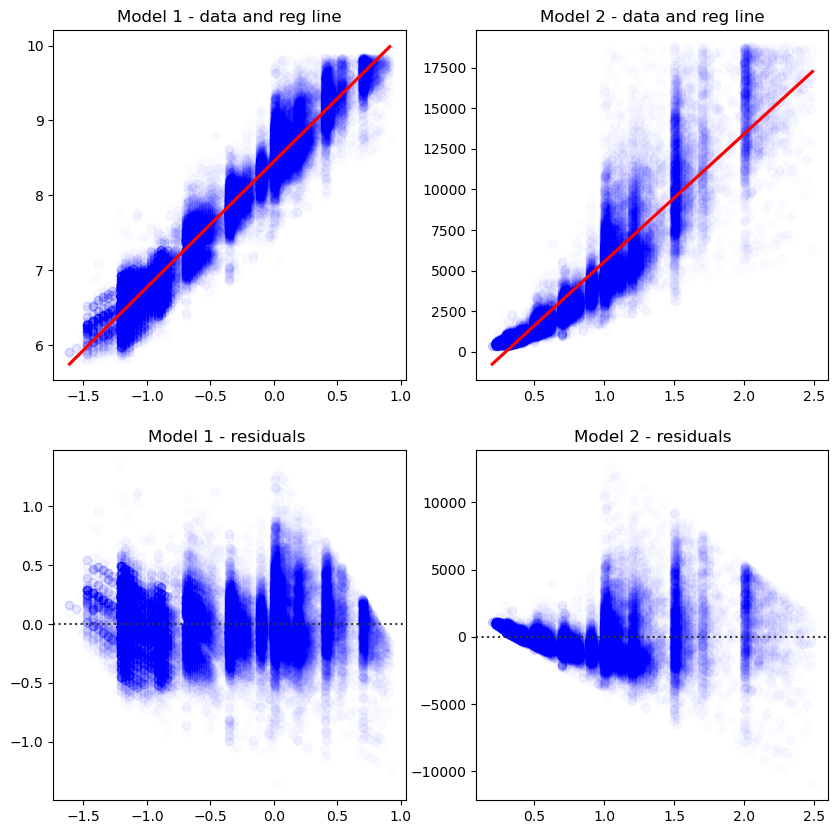
A key goal of just about any model is describing the data. In other words, how well does the model explain the data?
Intuitively, you look at these graphs and know that Model 1 describes the data better.
# load some data to practice regressions
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols as sm_ols
diamonds = sns.load_dataset('diamonds')
# this alteration is not strictly necessary to practice a regression
# but we use this in livecoding
np.random.seed(400)
diamonds2 = (diamonds
.assign(lprice = np.log(diamonds['price']),
lcarat = np.log(diamonds['carat']),
ideal = diamonds['cut'] == 'Ideal',
lprice2 = lambda x: x.lprice + 2*np.random.randn(len(diamonds))
)
.query('carat < 2.5') # censor/remove outliers
# some regression packages want you to explicitly provide
# a variable for the constant
.assign(const = 1)
)
fig, axes = plt.subplots(2,2,figsize = (10,10))
sns.regplot(data=diamonds2,ax=axes[0,0],y='lprice',x='lcarat',
scatter_kws = {'color': 'blue', 'alpha': 0.01},
line_kws = {'color':'red'},
).set(xlabel='',ylabel='',title='Model 1 - data and reg line')
sns.regplot(data=diamonds2,ax=axes[0,1], y='price',x='carat',
scatter_kws = {'color': 'blue', 'alpha': 0.01},
line_kws = {'color':'red'},
).set(xlabel='',ylabel='',title='Model 2 - data and reg line')
sns.residplot(data=diamonds2,ax=axes[1,0],y='lprice',x='lcarat',
scatter_kws = {'color': 'blue', 'alpha': 0.01},
line_kws = {'color':'red'},
).set(xlabel='',ylabel='',title='Model 1 - residuals ')
sns.residplot(data=diamonds2,ax=axes[1,1], y='price',x='carat',
scatter_kws = {'color': 'blue', 'alpha': 0.01},
line_kws = {'color':'red'},
).set(xlabel='',ylabel='',title='Model 2 - residuals')
plt.show()
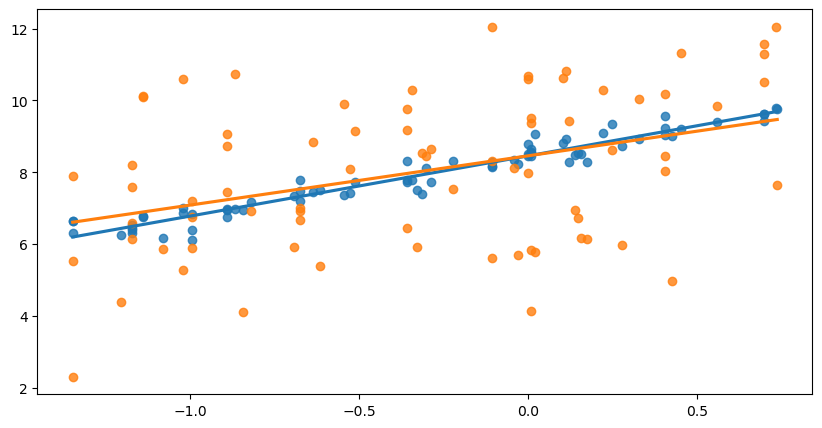
The next graph shows two different y variables (shown in blue and orange). Again, it’s fairly obvious that the blue points are better explained by the blue line than the orange is by the orange line.
fig, ax = plt.subplots(figsize = (10,5))
sns.regplot(x='lcarat',y='lprice',ax=ax,
data=diamonds2.sample(75,random_state=20),ci=None)
sns.regplot(x='lcarat',y='lprice2',ax=ax,
data=diamonds2.sample(75,random_state=20),ci=None)
plt.xlabel("")
plt.ylabel("")
plt.show()
The way we can capture that statistically is by computing R\(^2\).
Step 1: The total sum of squares: TSS \(= \sum_i (y_i - \bar{y}_i)^2\) captures the total amount of variation in \(y\) around its mean \(\bar{y}\). We’d like to explain as much of this as possible.
Step 2: The sum of squared errors: SSE \(= \sum_i (y_i - \hat{y}_i)^2\) captures the total amount of errors in the predictions. We’d like this to be as close to zero.
Step 3: \(SSE/TSS\) = The fraction of variation in y that a model can’t explain
Note
\(R^2 = 1-SSE/TSS\) = The fraction of variation in y that a model can explain
Statsmodels reports R\(^2\) and Adjusted R\(^2\) by default with .summary().
Let’s confirm that Model 1 > Model 2, and that Blue > Orange:
from statsmodels.iolib.summary2 import summary_col # nicer tables
# fit the two regressions, and save these as objects (containing the results)
res1 = sm_ols('lprice ~ lcarat',data=diamonds2).fit()
res2 = sm_ols('price ~ carat',data=diamonds2).fit()
res3 = sm_ols('lprice ~ lcarat',data=diamonds2).fit()
res4 = sm_ols('lprice2 ~ lcarat',data=diamonds2).fit()
# now I'll format an output table
# I'd like to include extra info in the table (not just coefficients)
info_dict={'R-squared' : lambda x: f"{x.rsquared:.2f}",
'Adj R-squared' : lambda x: f"{x.rsquared_adj:.2f}",
'No. observations' : lambda x: f"{int(x.nobs):d}"}
# This summary col function combines a bunch of regressions into one nice table
print(summary_col(results=[res1,res2,res3,res4],
float_format='%0.2f',
stars = True,
model_names=['Model 1','Model 2','Blue','Orange'],
info_dict=info_dict,
#regressor_order=[ # you can specify which variables you
# want at the top of the table here]
)
)
====================================================
Model 1 Model 2 Blue Orange
----------------------------------------------------
Intercept 8.45*** -2335.81*** 8.45*** 8.45***
(0.00) (12.98) (0.00) (0.01)
R-squared 0.93 0.85 0.93 0.19
R-squared Adj. 0.93 0.85 0.93 0.19
carat 7869.89***
(14.14)
lcarat 1.68*** 1.68*** 1.69***
(0.00) (0.00) (0.01)
R-squared 0.93 0.85 0.93 0.19
Adj R-squared 0.93 0.85 0.93 0.19
No. observations 53797 53797 53797 53797
====================================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01

6.3.1. One more example¶
Here is a dataset showing how many coins some people have in their wallet, and the value of each:
# Attribution: Example from UNKNOWN via @joshua_t_white (https://twitter.com/joshua_t_white/status/1655717884075581447)
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.iolib.summary2 import summary_col
# Set the seed for reproducibility
np.random.seed(0)
# Create a dataset with 30 observations
wallets = pd.DataFrame({
'quarters': np.random.randint(0, 11, 30),
'dimes': np.random.randint(0, 11, 30),
'nickels': np.random.randint(0, 11, 30),
'pennies': np.random.randint(0, 11, 30)
})
wallets.eval('total_value = 0.25*quarters + 0.1*dimes + 0.05*nickels + 0.01*pennies',inplace=True)
display(wallets.head(10))
| quarters | dimes | nickels | pennies | total_value | |
|---|---|---|---|---|---|
| 0 | 5 | 0 | 4 | 10 | 1.55 |
| 1 | 0 | 2 | 9 | 7 | 0.72 |
| 2 | 3 | 3 | 10 | 5 | 1.60 |
| 3 | 3 | 8 | 10 | 5 | 2.10 |
| 4 | 7 | 1 | 8 | 0 | 2.25 |
| 5 | 9 | 3 | 1 | 1 | 2.61 |
| 6 | 3 | 3 | 1 | 5 | 1.15 |
| 7 | 5 | 3 | 7 | 9 | 1.99 |
| 8 | 2 | 7 | 9 | 3 | 1.68 |
| 9 | 4 | 0 | 9 | 0 | 1.45 |
Look at Model 1 below. When we regress total_value on the number of all of the coins, the regression coefficients uncover the value of each type of coin perfectly: R\(^2\) is 1 and the coefficients are measured without any error.
But in Model 2, we don’t include quarters. This causes R\(^2\) to fall all the way to 0.22, because in this dataset, the value of quarters is responsible for most of the value of each wallet.
The other important thing to notice in Model 2 is what happens to the coefficient on the value of nickels and pennies: They are negative! When your regression omits a variable that is in the “true model” generating the data, it will bias the coefficients on other variables.
res1= sm_ols('total_value ~ quarters + dimes + nickels + pennies',data=wallets).fit()
res2= sm_ols('total_value ~ dimes + nickels + pennies',data=wallets).fit()
res3= sm_ols('total_value ~ quarters + nickels + pennies',data=wallets).fit()
res4= sm_ols('total_value ~ quarters + dimes + pennies',data=wallets).fit()
res5= sm_ols('total_value ~ quarters + dimes + nickels ',data=wallets).fit()
# Format the output table
info_dict = {'No. observations': lambda x: f"{int(x.nobs):d}"}
# Display the summary table
summary_table = summary_col(results=[res1,res2,res3,res4,res5],
float_format='%0.2f',
stars=True,
model_names=['Model 1','Model 2','Model 3','Model 4','Model 5'],
info_dict=info_dict,
regressor_order=['quarters', 'dimes', 'nickels', 'pennies'])
display(summary_table)
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
|---|---|---|---|---|---|
| quarters | 0.25*** | 0.25*** | 0.23*** | 0.25*** | |
| (0.00) | (0.02) | (0.01) | (0.00) | ||
| dimes | 0.10*** | 0.10** | 0.10*** | 0.10*** | |
| (0.00) | (0.04) | (0.01) | (0.00) | ||
| nickels | 0.05*** | -0.04 | 0.05** | 0.05*** | |
| (0.00) | (0.04) | (0.02) | (0.00) | ||
| pennies | 0.01*** | -0.03 | 0.01 | 0.01 | |
| (0.00) | (0.04) | (0.02) | (0.01) | ||
| Intercept | 0.00 | 1.92*** | 0.37 | 0.38*** | 0.06** |
| (0.00) | (0.34) | (0.23) | (0.08) | (0.02) | |
| R-squared | 1.00 | 0.22 | 0.83 | 0.97 | 1.00 |
| R-squared Adj. | 1.00 | 0.13 | 0.81 | 0.96 | 1.00 |
| No. observations | 30 | 30 | 30 | 30 | 30 |
